قوانین حرکت نیوتن

«قوانین حرکت نیوتن» (Newton’s Laws Of Motion) کدام است و چه کاربردی دارد؟ در این نوشته به قوانین اول، دوم و سوم نیوتن می‌پردازیم. در ادامه برای فهم بهتر، مثال‌هایی کاربردی نیز ارائه می‌شود.

قانون اول نیوتن

قانون اول نیوتن بیان می‌کند که اگر هیچ نیروی خالص خارجی بر روی یک جسم بدون حرکت وارد نشود، این جسم همچنان بی‌حرکت باقی می‌ماند. در تعریفی دیگر می‌توان گفت، بدون اعمال نیروی خالص خارجی بر روی جسمی که در یک مسیر مستقیم با سرعت ثابت در حرکت است‌، جسم همچنان به حرکت مستقیم خود در سرعت ثابت ادامه می‌دهد.

قانون دوم نیوتن

قانون دوم نیوتن بیان می‌کند که مجموع نیروهای وارده بر جسم برابر با شتابی است که متناسب با جرم ذره به آن اعمال می‌گردد.

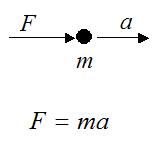
در این معادله:

F: نیروی اعمال شده بر ذره

m: جرم ذره

a: شتاب ذره در جهت اعمال نیرو بر آن با توجه به دستگاه یا چارچوب مرجع لخت

قانون دوم نیوتن را برای سیستمی از مجموعه ذرات نیز به شکل زیر می‌توان عنوان کرد.

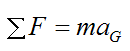
ΣF مجموع بردار نیروهای خارجی است که بر روی سیستم ذرات وارد می‌شوند. به این مجموع گاهی نیروی خالص خارجی می‌گویند.

در این معادله:

m مجموع جرم سیستم ذرات

a_G شتاب مرکز جرم سیستم ذرات (با توجه به دستگاه یا چارچوب مرجع لخت) است. شتاب و نیروهای وارد شده بر جسم هم‌جهت هستند.

توجه داشته باشید که هیچ محدودیتی در روش اتصال ذرات وجود ندارد. در نتیجه، معادله فوق برای اجسام سخت، جسم بی‌شکل و نامنظم، سیستم مایع و گاز درست است.

قانون سوم نیوتن

سومین قانون حرکت نیوتن به این صورت بیان می‌شود که هر عملی را عکس‌العملی است، مساوی با آن و در جهت خلاف آن. تصور کنید جسم یک و دو در تماس با هم هستند. هرگاه جسم یک به جسم دو نیرو وارد کند، جسم دوم نیز نیرویی به همان بزرگی ولی در خلاف جهت بر جسم یک وارد می‌کند.

تصویر زیر دو جسم در تماس با هم را نشان می‌دهد.

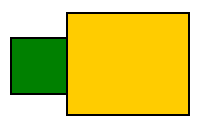
اگر دو جسم را به صورت جداگانه در نظر بگیریم، نیروهای وارد شده به هر دو جسم از لحاظ بزرگی برابر و دارای جهات مختلف هستند. شکل زیر مثالی کلی از نیروهای وارده به هر جسم را نشان می‌دهد.

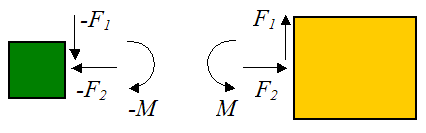
F1 نیروی عمودی برآیند، F2 نیروی افقی برآیند و M «گشتاور» (torque) برآیند در سطح تماس است. نیروی عمودی برآیند وارد شده به جسم برابر با مجموع نیروهایی است که در جهت عمودی بر سطح وارد می‌شوند. نیروی افقی برآیند وارد شده به جسم برابر با مجموع نیروهایی است که در جهت افقی بر سطح وارد می‌شوند. گشتاور برآیند وارد شده به جسم برابر با مجموع گشتاورهایی است که در طول سطح تماس به آن وارد می‌گردد.

با اعمال نیروهای مساوی در جهات مخالف هم، گشتاور ایجاد می‌شود. به عنوان مثال، شکل زیر نشان‌ دهنده‌ی نیروهای برابر Fc است. این نیروها در جهت مخالف (بر روی هر یک از اجسام) عمل می‌کند و توسط فاصله R به شکل عمودی از هم جدا می‌شود.

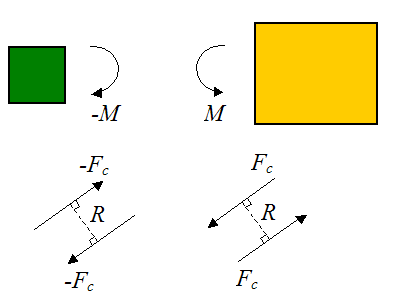
پس گشتاور به صورت زیر محاسبه می‌گردد:

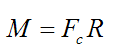
گشتاور M باعث چرخش خالص جسم می‌گردد. پارامتر M یا گشتاور در موازنه‌ی نیرو (F = ma) مربوط به قانون دوم نیوتن وجود ندارد. در عوض در محاسبه موازنه‌ی گشتاور، این نیرو به کار گرفته می‌شود.

به طور کلی، هنگام حل مسائل فیزیک دنیای واقعی، هر سطح تماس (یا نقطه تماس) بین یک جسم و یک جسم دیگر می‌تواند با یک نیروی برآیند F به اجزای آن، شامل نیروی افقی و عمودی، تفکیک گردد. (همان‌طور که در شکل بالا نشان داده شده است) در ادامه گشتاور M جایگزین می‌شود. این نیرو و مومنتوم از لحاظ بزرگی برای هر دو جسم با هم برابر ولی جهت آن‌ها مخالف است.

توجه داشته باشید در بعضی موارد، تنها نیروی برآیند F یا گشتاور برآیند M، بر سطح تماس وارد می‌شود. اگرچه، شاید نتوان تشخیص داد که کدام یک واقعا وجود دارد. بنابراین، باید از طریق حل محاسبات دینامیکی به آن پی برد.

برای مثال، «مفصل توپی یا گوی و کاسه‌ای» (Ball and socket joint) نمی‌تواند در برابر پیچ‌خوردگی مقاوم باشد. بنابراین، هیچ گشتاوری وجود ندارد. اما در برابر کشیدن و هل دادن مقاوم است. پس، یک نیروی برآیند F بر سطح تماس (بین گوی و کاسه مفصل) ایجاد می‌گردد. از سوی دیگر، به برخی از سطوح تماس فقط گشتاور برآیند M (چرخش خالص) وارد می‌شود. یک مثال از این مورد، دسته‌ی آچار پیچ‌گوشتی است.

مزیت اصلی جابه‌جایی یک سطح تماس (یا نقطه تماس) تنها با نیروی برآیند F و یا گشتاور برآیند M، راحتی در معادلات ریاضی است. بدین طریق معادله‌های دینامیکی به روشی ساده و ممکن حل می‌شوند. راه حل دیگر به این شکل است: حرکت کلی یک جسم همیشه شامل حرکت انتقالی و چرخشی است. نیروی برآیند F وارد شده به جسم، باعث انتقال (بسته به جایی که نیرو وارد می‌شود) و چرخش می‌گردد. گشتاور برآیند M اعمال شده به جسم، به چرخش جسم کمک می‌کند.

با این حساب، نیروها هم در معادلات نیرو (F = ma) و هم معادلات گشتاور نقش دارند. اما موارد مربوط به گشتاور فقط در معادلات مربوط به گشتاور قرار می‌گیرند. از این نمونه به فیزیک چرخش توپ گلف می‌توان اشاره کرد.

منبع: فرادرس